Tabular Playground Series 比赛 去噪和quantile normalization

原文，利用自编码器去噪。

1. 导入包和数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import random, math, sys
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from pathlib import Path
import seaborn as sns
import tensorflow as tf
import tensorflow.keras.backend as K
from tensorflow import keras
from tensorflow.keras import layers, initializers, regularizers, activations, callbacks
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.models import Model
import tensorflow_addons as tfa

from sklearn.model_selection import KFold, StratifiedKFold
from sklearn.preprocessing import StandardScaler, scale
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA
import warnings
warnings.simplefilter('ignore')

使用版本信息:

1
2
3
4
5
print(tf.__version__)
print(keras.__version__)
===========================
2.4.1
2.4.0

导入数据：

1
2
3
4
5
6
7
8
9
10
11
12
13
data_dir = Path("/data")
train = pd.read_csv(data_dir/'train.csv')
test = pd.read_csv(data_dir/'test.csv')
sample = pd.read_csv(data_dir/'sample_submission.csv')
train.drop(['id'], axis=1, inplace=True)
test.drop(['id'], axis=1, inplace=True)
y = np.array(train['loss'])
X = train.drop(['loss'], axis=1)
xall = pd.concat([X, test], axis=0, copy=False).reset_index(drop=True)
#print(xall.head())
print(X.shape, y.shape, test.shape, xall.shape)
==================================================
(250000, 100) (250000,) (150000, 100) (400000, 100)

2. quantile normalize

Quantile_normalization解释，用它处理数据来得到相同分布。具体来说：

  1. 先分级，如例子中基因的数目为4就分为4个级别。
1
2
3
4
A    5    4    3
B    2    1    4
C    3    4    6
D    4    2    8

对应分配级别i-iv，记下对应的rank

1
2
3
4
A    iv    iii   i
B    i     i     ii
C    ii    iii   iii
D    iii   ii    iv
  1. 对原始数据的按特征列排序。
1
2
3
4
A    5    4    3    becomes A 2 1 3
B    2    1    4    becomes B 3 2 4
C    3    4    6    becomes C 4 4 6
D    4    2    8    becomes D 5 4 8
  1. 对排序后的数据进行每行求均值
1
2
3
4
A (2 + 1 + 3)/3 = 2.00 = rank i
B (3 + 2 + 4)/3 = 3.00 = rank ii
C (4 + 4 + 6)/3 = 4.67 = rank iii
D (5 + 4 + 8)/3 = 5.67 = rank iv
  1. 我们再按1中的对应的rank填入对应值, 到这儿就是quantile normalize算法过程。
1
2
3
4
A    5.67    4.67    2.00
B    2.00    2.00    3.00
C    3.00    4.67    4.67
D    4.67    3.00    5.67

实际过程中，步骤4中的第二列，有两个一样值4.67，这是要避免的，你要把每列都同分布嘛，就取和最靠近的哪个rank对应值的平均值。这就是具体quantile normalize过程，最后结果如下：

1
2
3
4
A    5.67    5.17    2.00
B    2.00    2.00    3.00
C    3.00    5.17    4.67
D    4.67    3.00    5.67

在该数据集中，我们直接先对原始数据进行类似最大最小化的75分位数25分位处理，来避免分位数归一化中的同数情况。#TODO

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
xmedian = pd.DataFrame.median(xall, 0)
x25quan = xall.quantile(0.25, 0)
x75quan = xall.quantile(0.75, 0)
xall = (xall- xmedian)/(x75quan-x25quan)

def quantile_norm(df_input):
    """分位数标准化"""
    #对df_input按每行值进行升序排序
    sorted_df = pd.DataFrame(np.sort(df_input.values, axis=0), index=df_input.index, columns=df_input.columns)
    mean_df = sorted_df.mean(axis=1)#排序均值
    mean_df.index = np.arange(1, len(mean_df) + 1)#分级
    quantile_df = df_input.rank(axis=0, method='min').stack().astype('int').map(mean_df).unstack()
    return (quantile_df)

qall = np.array(quantile_norm(xall))#将xall进行分位数标准化后作为array
qlabeled = qall[:len(train), :] #取train长度行作为标记的data
qunlabled = qall[len(train):, :]

拿 quantile_norm(df_input)实验一下wiki例子：

1
2
3
4
5
6
7
8
xall = pd.DataFrame([[5, 4, 3], [2, 1, 4], [3, 4, 6], [4, 2, 8]])
qall = np.array(quantile_norm(xall))
print(qall)
=============================================
[[5.66666667 4.66666667 2.        ]
 [2.         2.         3.        ]
 [3.         4.66666667 4.66666667]
 [4.66666667 3.         5.66666667]]

3. creation bins

创建箱分位数据来进一步增加数据输入多样性。

1
2
3
4
5
6
7
ball = np.zeros((qall.shape[0], X.shape[1])) #创建qall.shape行数 X.shape列数的全0矩阵来存储
for i in range(X.shape[1]):
    #取第i列，按照X.shape[1]分箱 无标签 重复出现丢掉
    ball[:, i] = pd.qcut(qall[:, i], X.shape[1], labels=False, duplicates='drop')
blabled = ball[:X.shape[0], :]
bunlabled = ball[X.shape[0]:, :]

例如拿wiki例子中数据，就是上面 [5.66666667 4.66666667 2. ]这个矩阵， 来处理下有:

1
2
3
4
5
6
7
8
9
ball = np.zeros((qall.shape[0], qall.shape[1]))
for i in range(qall.shape[1]):
    ball[:, i] = pd.qcut(qall[:, i], qall.shape[1], labels=False, duplicates='drop')
print(ball)
===================================
[[2. 1. 0.]
 [0. 0. 0.]
 [0. 1. 1.]
 [1. 0. 2.]]

4. denoise Autoencoder

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#噪声生成为0, 0.1的正态分布，size指定
noise = np.random.normal(0, .1, (qall.shape[0], qall.shape[1]))
qall = np.array(qall)
xnoisy = qall + noise
limit = np.int(0.8 * qall.shape[0])#用来划分训练集和验证集
xtrain = xnoisy[0:limit, :]
ytrain = qall[0:limit, ]
xval = xnoisy[limit:qall.shape[0], :]
yval = qall[limit:qall.shape[0], :]
print(xtrain.shape, ytrain.shape, xval.shape, yval.shape)
======================================================
(320000, 100) (320000, 100) (80000, 100) (80000, 100)

#早停和衰减策略
es = tf.keras.callbacks.EarlyStopping(
    monitor='val_loss',
    min_delta=1e-9, #最小变化阈值
    patience=20,
    verbose=0,
    mode='min',
    baseline=None,
    restore_best_weights=True
)

plateau = tf.keras.callbacks.ReduceLROnPlateau(
    monitor='val_loss',
    factor=0.8,
    patience=4,
    verbose=0.,
    mode='min'
)

def custom_loss(y_true, y_pred):
    loss = K.mean(K.square(y_pred - y_true))
    return loss

def autoencoded():
    ae_input = layers.Input(shape=(qall.shape[1]))
    ae_encoded = layers.Dense(units=qall.shape[1], activation='elu')(ae_input)
    ae_encoded = layers.Dense(units=qall.shape[1]*3, activation='elu')(ae_encoded)
    ae_decoded = layers.Dense(units=qall.shape[1], activation='elu')(ae_encoded)

    return Model(ae_input, ae_decoded), Model(ae_input, ae_encoded)


autoencoder, encoder = autoencoded()
autoencoder.compile(loss=custom_loss,
            optimizer=keras.optimizers.Adam(lr=5e-3))


自编码器的总结:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
autoencoder.summary()
===========================
Model: "model"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_1 (InputLayer)         [(None, 100)]             0         
_________________________________________________________________
dense (Dense)                (None, 100)               10100     
_________________________________________________________________
dense_1 (Dense)              (None, 300)               30300     
_________________________________________________________________
dense_2 (Dense)              (None, 100)               30100     
=================================================================
Total params: 70,500
Trainable params: 70,500
Non-trainable params: 0

训练自编码器

1
2
3
4
5
6
7
8
9
10
history = autoencoder.fit(xtrain, ytrain,
            epochs=200,
            batch_size=512,
            verbose=0,
            validation_data=(xval, yval),
            callbacks=[es, plateau])
            
eall = encoder.predict(qall) #data 用去噪编码器编a码
print("max encoded value = ", np.max(eall))#max encoded value =  10.96393   
print(eall.shape)# (400000, 300)

5. 根据方差阈值特征编码选择特征

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
evar = np.var(eall, axis=0, ddof=1) #ddof=1计算总体方差时除以n-1,0时除以n
evar1 = evar > 0.8
a = np.where(evar1 == False, evar1, 1)#满足evar1 == False为真，a=evar1/0, 反之为1
nb_col = a.sum()#100

#构建3倍特征列df， 列名变为f'col_{i}'
eall_1 = pd.DataFrame()
for i in range(qall.shape[1] * 3):
    if evar1[i] == True:
        colname = f'col_{i}'
        eall_1[colname] = eall[:, i]
        
eall_1 = np.array(eall_1)
elabeled = eall_1[:len(train), :]
eunlabeled = eall_1[len(train):, :]
elabeled.shape, eunlabeled.shape
=================================
((250000, 100), (150000, 100))

6. 对编码特征进行PCA降维再标准化

1
2
3
4
pca = PCA(n_components=15)
pall = pca.fit_transform(eall)
sc_pca = StandardScaler()
pall = sc_pca.fit_transform(pall)

7.合并PCA降维后特征和编码特征(方差阈值之后)

1
2
3
4
plabled = pall[:len(train), :]
punlabled = pall[len(train):, :]
elabeled = np.hstack((elabeled, plabled)) #水平拼接特征形成elabeled:plabled
eunlabeled = np.hstack((eunlabeled, punlabled))

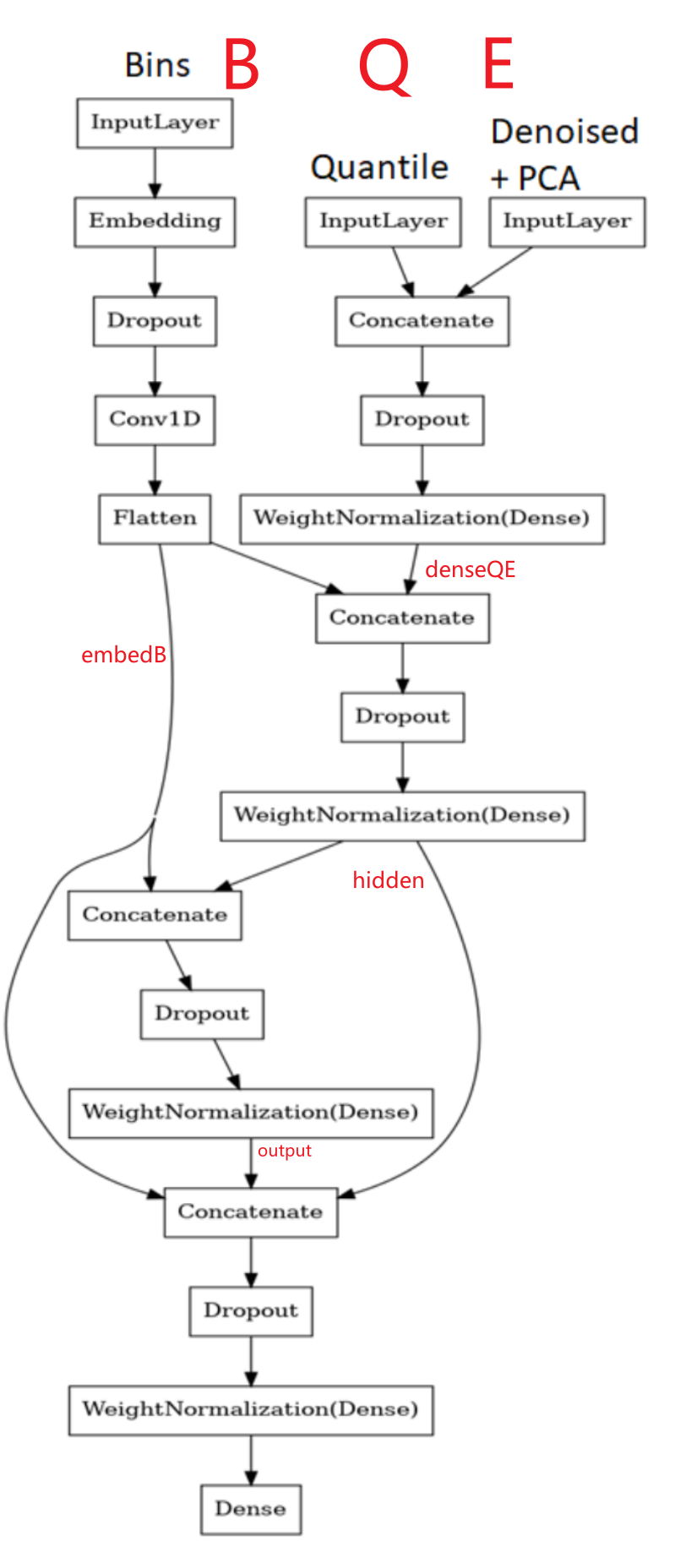
8. 构建残差模型来解决任务

这块很有意思搭建多残差网络，根据图来理解

Snipaste_2021-08-20_18-59-23

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
# NN Model
def get_res_model():
    #分位数标准化输入
    inputQ = layers.Input(shape=(qall.shape[1]))
    #encoded+PCA后输入
    inputE = layers.Input(shape=(elabeled.shape[1]))
    #箱型输入
    inputB = layers.Input(shape=(blabled.shape[1]))

    #第一路 前馈网络 先合并QE在dropout
    denseQE = layers.Dropout(0.3)(layers.Concatenate()([inputQ, inputE]))
    denseQE = tfa.layers.WeightNormalization(layers.Dense(
        units=300,
        activation='elu',
        kernel_initializer='lecun_normal'
    ))(denseQE)

    #第二路: enbedding + conv block 先embedding
    embedB = layers.Embedding(input_dim=blabled.shape[1] + 1,
                              output_dim=6,
                              embeddings_regularizer='l2',
                              embeddings_initializer='lecun_uniform')(inputB)

    embedB = layers.Dropout(0.3)(embedB)
    embedB = layers.Conv1D(6, 1, activation='relu')(embedB)
    embedB = layers.Flatten()(embedB)

    # 残差网络结构， 先合并两路输出
    hidden = layers.Dropout(0.3)(layers.Concatenate()([denseQE, embedB]))
    hidden = tfa.layers.WeightNormalization(layers.Dense(
        units=64, activation='elu', kernel_initializer='lecun_normal'
    ))(hidden)

    #输出合并第一次
    output = layers.Dropout(0.3)(layers.Concatenate()([embedB, hidden]))
    output = tfa.layers.WeightNormalization(
        layers.Dense(units=32, activation='relu', kernel_initializer='lecun_normal')
    )(output)

    #输出再合并
    output = layers.Dropout(0.4)(layers.Concatenate()([embedB, hidden, output]))
    output = tfa.layers.WeightNormalization(layers.Dense(
        units=32, activation='selu', kernel_initializer='lecun_normal'
    ))(output)
    output = layers.Dense(units=1, activation='selu',\
                          kernel_initializer='lecun_normal')(output)
    
    model = Model([inputQ, inputE, inputB], output)
    model.compile(loss='mse',
                  metrics=[tf.keras.metrics.RootMeanSquaredError()],
                  optimizer=keras.optimizers.Adam(lr=0.005))

    return model
# nn_model = get_res_model()
# tf.keras.utils.plot_model(nn_model, to_file='./dense.png', show_shapes=False, show_layer_names=True)

9. 训练模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
N_FOLDS = 10
SEED = 1
EPOCH = 100
N_ROUND = 5
oof = np.zeros((y.shape[0], 1))
pred = np.zeros((test.shape[0], 1))

for i in range(N_ROUND):
    oof_round = np.zeros((y.shape[0], 1)) #构建每轮
    skf = StratifiedKFold(n_splits=N_FOLDS,
                          shuffle=True,
                          random_state=SEED*i)
    for fold, (tr_idx, ts_idx) in enumerate(skf.split(X, y)):
        print(f"\n ---------Training Round {i+1} Fold {fold+1} ----\n")
        #标准化
        qtrain = qlabeled[tr_idx]
        qval = qlabeled[ts_idx]
        
        #Binned
        btrain = blabled[tr_idx]
        bval= blabled[ts_idx]
        
        #encoded
        etrain = elabeled[tr_idx]
        eval = elabeled[ts_idx]
        
        #target
        ytrain = y[tr_idx]
        yval = y[ts_idx]
        
        K.clear_session()
        
        #模型训练
        nn_model = get_res_model()
        nn_model.fit([qtrain, etrain, btrain],
                  ytrain,
                  batch_size=2048,
                  epochs=EPOCH,
                  validation_data=([qval, eval, bval], yval),
                  callbacks=[es, plateau],
                  verbose=1)
        
        nn_model.save(data_dir/f'model{i}.ckpt')
        #预测
        pred_round = nn_model.predict([qval, eval, bval])
        oof[ts_idx] += pred_round / N_ROUND#预测值/轮数
        oof_round[ts_idx] += pred_round
        
        pred += nn_model.predict([qunlabled, eunlabeled, bunlabled]) / (N_FOLDS * N_ROUND)
    score_round = math.sqrt(mean_squared_error(y, oof_round))
    print(f"第{i+1}轮分数{score_round}=====\n")
score_round = math.sqrt(mean_squared_error(y, oof))
print(f"最终分数{score_round}=====\n")
10. 预测
1
2
3
4
5
6
sample_submission = pd.read_csv(data_dir/'sample_submission.csv')
sample_submission['pred'] = pred
pd.DataFrame(oof).to_csv('oof.csv', index=False)
sample_submission.to_csv('sb1.csv', index=False)
display(pd.read_csv('sb1.csv'))